Long Live the C: Arrays and Memory
Arrays are the objects that are stored contiguously in memory.
CPU Caches, Multithreading and False Sharing, Scott Meyers’ example
Scott Meyers showed the significance of CPU caches with two examples in his talk “CPU Caches and Why You Care.” The first example illustrates how the order of row- and column-traversal can drastically affect the access time of a 2-dimensional array. In the second example, Meyers shows the advantages of employing local variables in a multithreading environment over accessing a “global” variable.
In this post, my goal is to recreate these two examples in C, investigating whether similar behavior exists within the context of C programming. As high-level programmers, we may not have direct control over how CPU caches interact with main memory, but by aligning our code with the principles governing cache operation, we can significantly enhance program efficiency.
Let’s start from a few key concepts about CPU caches that we should bear in mind to better understand the two examples. A graph of the minimum configuration of cache is shown below.
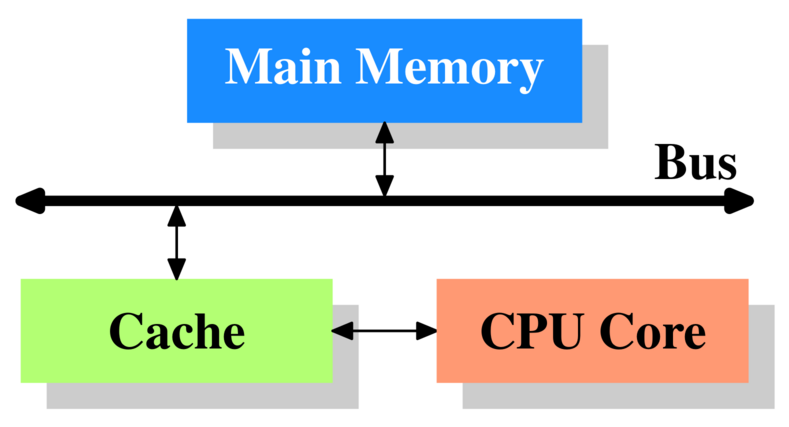Minimum Cache Configuration adapted from Figure 3.1 in "What Every Programmer Should Know About Memory."
- The CPU core doesn’t directly communicate with the main memory. Instead, it relies on an intermediary called the cache.
- Data transfer between the main memory and the cache occurs in fixed-size blocks known as “cache lines.” These cache lines are essential for efficient data retrieval and storage.
- The latency of CPU caches is notably lower, typically by one to two orders of magnitude when compared to the main memory.
- When the processor needs to read or write a location in memory, it first checks if the memory location is in the cache. If the processor finds that the memory location is in the cache, a cache hit has occurred. It reads or writes immediately from the cache line.
- On the other hand, if the processor does not find the memory location in the cache, a cache miss has occurred. It then retrieves the data from the main memory to the cache line. This retrieval process is significantly slower compared to accessing data directly from the cache line as explained above.
A Tale of Two Traversals
The first example involves traversing a 2D array using row-major and column-major order.
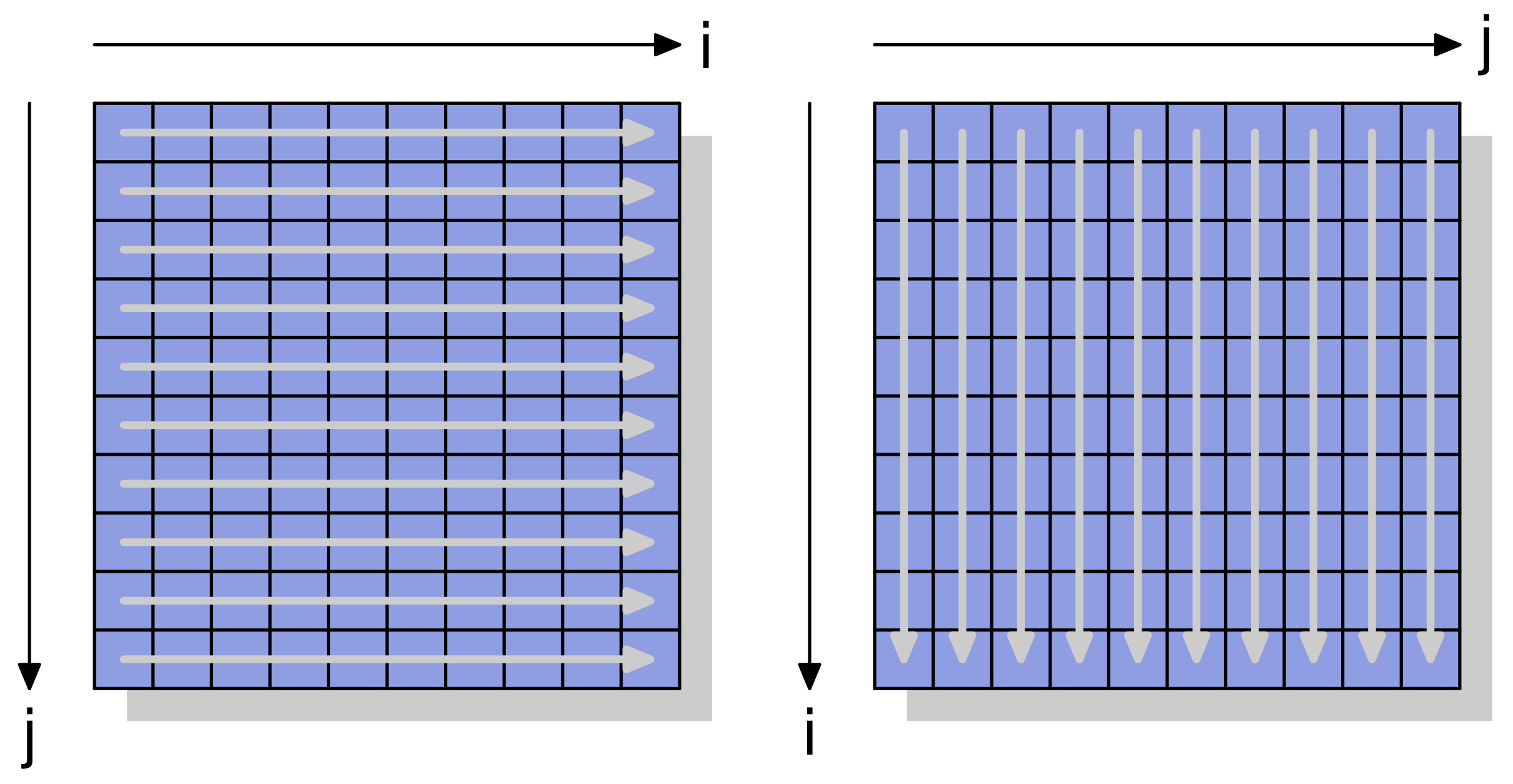Row-wise and column-wise traversal of a 2D array. The graph is adapted from Figure 6.1 in "What Every Programmer Should Know About Memory."
Below is the C code snippet that defines a global array and the corresponding traversal function:
#include <stdio.h>
#include <string.h>
#include <time.h>
#include <assert.h>
// Define as global because the size cannot fit in the stack.
int num_row = 65536;
int num_col = 4096;
int arr[65536][4096] = 0;
long long sum_2d_array(size_t num_row, size_t num_col, int arr[num_row][num_col],
const char *traversal_order) {
long long sum = 0;
if (strcmp(traversal_order, "row_major") == 0) {
for (size_t r = 0; r < num_row; ++r) {
for (size_t c = 0; c < num_col; ++c) {
sum += arr[r][c];
}
}
} else {
for (size_t c = 0; c < num_col; ++c) {
for (size_t r = 0; r < num_row; ++r) {
sum += arr[r][c];
}
}
}
return sum;
}
In the if block, the code traverses row by row, whereas in the else block, it
traverses column by column. We can test this code with the following functions:
void write_2d_array(size_t num_row, size_t num_col, int arr[num_row][num_col]) {
for (size_t i = 0; i < num_row; ++i) {
for (size_t j = 0; j < num_col; ++j) {
arr[i][j] = j + i * num_col;
}
}
}
void print_2d_array(size_t num_row, size_t num_col, int arr[num_row][num_col]) {
for (size_t i = 0; i < num_row; ++i) {
for (size_t j = 0; j < num_col; ++j) {
printf("%d ", arr[i][j]);
}
printf("\n");
}
}
// gcc sum_2d_array.c && ./a.out
int main() {
struct timespec start, end;
double elapsed;
long long s1 = 0, s2 = 0;
write_2d_array(num_row, num_col, arr); // print_2d_array(num_row, num_col, arr);
clock_gettime(CLOCK_REALTIME, &start);
s1 = sum_2d_array(num_row, num_col, arr, "row_major");
clock_gettime(CLOCK_REALTIME, &end);
elapsed = (end.tv_sec - start.tv_sec) + (end.tv_nsec - start.tv_nsec) / 1e9;
printf("CPU time used of row-major order: %.3f seconds\n", elapsed);
clock_gettime(CLOCK_REALTIME, &start);
s2 = sum_2d_array(num_row, num_col, arr, "col_major");
clock_gettime(CLOCK_REALTIME, &end);
elapsed = (end.tv_sec - start.tv_sec) + (end.tv_nsec - start.tv_nsec) / 1e9;
printf("CPU time used of column-major order: %.3f seconds\n", elapsed);
assert(s1 == s2);
return 0;
}
The results are as follows:
CPU time used of row-major order: 0.442 seconds
CPU time used of column-major order: 2.357 seconds
Notably, the computed sum remains the same in both cases, but the time taken differs significantly. The row-wise traversal is about 5.3 times faster than the column-wise traversal. You might find this performance intriguing. It’s not immediately evident why a seemingly trivial difference in traversal order would lead to such a significant variation in execution time. The answer lies in a fundamental rule of CPU caches - cache lines.
Essentially, cache lines store the target byte and its neighboring bytes from memory. In
the case of row-wise traversal, when a thread accesses arr[0][0], the CPU loads the
adjacent bytes such as arr[0][1], arr[0][2], arr[0][3], and so on, into the same
cache line. Consequently, when it needs to access subsequent bytes following
arr[0][0], it can retrieve them from the cache rather than the main memory, resulting
in a cache hit. However, in the case of column-wise traversal, where arr[1][0] is the
next element to access after arr[0][0], it falls outside the boundaries of the cache
line, leading to a cache miss. This requires the CPU to retrieve arr[1][0] from the
main memory. This process repeats throughout the whole process, explaining why
column-wise traversal is considerably slower than its row-wise counterpart.
A Scalability Story
The second example is employing a multithreading program to count the occurences of odd numbers in a 2D array. In other words, we want to implement a multithreading program to achieve what the following single-threaded function does:
size_t sequential_counting(size_t num_row, size_t num_col, int arr[num_row][num_col]) {
size_t num_odds = 0;
for (size_t r = 0; r < num_row; ++r) {
for (size_t c = 0; c < num_col; ++c) {
if (arr[r][c] % 2 != 0) {
num_odds += 1;
}
}
}
return num_odds;
}
Here is the required data structure and our target function which will be run with multiple threads.
// Define a struct to pass thread-specific data
typedef struct {
int* arr;
size_t num_row;
size_t num_col;
size_t start_row;
size_t end_row;
size_t result;
} ThreadData;
void* count_odds_nonscalable(void* arg) {
ThreadData* data = (ThreadData*)arg;
for (size_t r = data->start_row; r < data->end_row; ++r) {
for (size_t c = 0; c < data->num_col; ++c) {
if (*(data->arr + r * data->num_col + c) % 2 != 0) {
data->result += 1;
}
}
}
pthread_exit(NULL);
}
Firstly, it uses row-wise traversal whose advantage has beed discussed above. Second,
for each thread, it only traverse from start_row till end_row. I.e., if 8 threads
are used and there are 16 rows in a 2D array, then each thread only needs to process 2
rows and stores the result into result. thus, the concurrency is implemented using
multithreading. Now, we can initialize the threads with the following code:
size_t concurrent_counting(size_t num_row, size_t num_col, int* p_arr,
int num_threads) {
pthread_t threads[num_threads];
ThreadData thread_data[num_threads];
size_t chunk_size = num_row / num_threads;
for (int p = 0; p < num_threads; ++p) {
thread_data[p].arr = p_arr;
thread_data[p].num_row = num_row;
thread_data[p].num_col = num_col;
thread_data[p].start_row = p * chunk_size;
thread_data[p].end_row = (p + 1) * chunk_size;
thread_data[p].result = 0;
pthread_create(&threads[p], NULL, count_odds_scalable, (void*)&thread_data[p]);
}
for (int p = 0; p < num_threads; ++p) {
pthread_join(threads[p], NULL);
}
size_t sum = 0;
for (int p = 0; p < num_threads; ++p) {
sum += thread_data[p].result;
}
return sum;
}
In this block of code, chunk_size is the number of rows each thread needs to process.
The first for loop initializes and activates all threads. The second for loop waits
for all threads to be finished. The third for loop gathers all information from each
element of thread_data. This code can be tested with:
// gcc -pthread count_multithread.c && ./a.out
int main() {
struct timespec start, end;
double elapsed;
int num_threads = 1;
write_2d_array(num_row, num_col, arr);
clock_gettime(CLOCK_REALTIME, &start);
// size_t num_odds = sequential_counting(num_row, num_col, arr);
size_t num_odds = concurrent_counting(num_row, num_col, &arr[0][0], num_threads);
clock_gettime(CLOCK_REALTIME, &end);
elapsed = (end.tv_sec - start.tv_sec) + (end.tv_nsec - start.tv_nsec) / 1e9;
printf("Using %d thread. CPU time used: %f milliseconds\n", num_threads, 1000 * elapsed);
assert (num_odds == 134217728);
return 0;
}
The result is:
Non-scalable multi-threaded function:
Using 1 thread. CPU time used: 501.155763 milliseconds
Using 2 thread. CPU time used: 595.404849 milliseconds
Using 4 thread. CPU time used: 435.936983 milliseconds
Using 8 thread. CPU time used: 315.120970 milliseconds
Using 16 thread. CPU time used: 252.711079 milliseconds
Surprisingly, the time taken when using 16 threads is only half of the time taken when using a single thread. Even more perplexing, using just two threads takes more time than using a single thread. This outcome might leave you wondering, “Why bother with multithreading at all?”
To address this conundrum, we introduce a scalable multithreading implementation for counting odd numbers.
void* count_odds_scalable(void* arg) {
ThreadData* data = (ThreadData*)arg;
size_t num_odds = 0; // Create a local variable to store temporary result.
for (size_t r = data->start_row; r < data->end_row; ++r) {
for (size_t c = 0; c < data->num_col; ++c) {
if (*(data->arr + r * data->num_col + c) % 2 != 0) {
num_odds += 1; // Write to the local variable as opposed to `data->result`.
}
}
}
data->result = num_odds; // Assign `num_odds` to `data->result`.
pthread_exit(NULL);
}
The crucial modification here is the use of a local variable num_odds to store the
temporary result instead of directly writing to data->result. This seemingly minor
change can significantly impact the performance of our program. The result is
Scalable multi-threaded function:
Using 1 thread. CPU time used: 468.278321 milliseconds
Using 2 thread. CPU time used: 233.655324 milliseconds
Using 4 thread. CPU time used: 125.719726 milliseconds
Using 8 thread. CPU time used: 69.907420 milliseconds
Using 16 thread. CPU time used: 59.278413 milliseconds
it shows that the scalability of the program appears to be nearly linear up to 16 threads. (But why does it plateau at this point? my hunch is about the number of available CPU cores (16 in my case). It’s not just the CPU count that influences scalability; other factors like concurrent processes, such as browsers and editors running on my laptop, play a significant role in this observed behavior.)
But why are we observing we are observing? In count_odds_nonscalable, we’re already
using row-major traversal, and thread_data is stored contiguously in main memory. Each
thread accesses different elements within the thread_data array, ensuring that there
are no race conditions over thread_data.
Now, let’s try a thought experiment. Imagine using only two threads, with
thread_data[0] and thread_data[1] dedicated to storing information for these
threads. While it may seem that concurrent access is thread-safe, a hidden issue
arises. It’s possible that thread_data[0] and thread_data[1] share the same cache
line. This phenomenon is known as false sharing.
False sharing occurs when different threads access data that shares a cache block with
data being modified by another thread. In our case, if one core modifies
thread_data[0] by incrementing it, it may invalidate the cache line in another core
containing thread_data[1]. As a result, the waiting core must reload the entire cache
block, even though it’s not logically necessary. The legitimate nature of our
count_odds_nonscalable function is not in question; the issue lies in cache
management.
On the other hand, when a local variable is used in the count_odds_scalable function,
it’s allocated on the stack for each thread. This approach effectively eliminates the
possibilities of false sharing. Stack allocation ensures that each thread works with its
own isolated copy of the variable, which doesn’t share cache lines with other threads.
This results in a significant reduction in cache coherency issues, allowing our
multithreaded program to run more efficiently and scale better, as each thread operates
independently without causing cache-related bottlenecks.
Conclusion: The mysteries of scalability in multithreading are closely tied to the interactions between CPU caches and the structure of data. False sharing, as demonstrated in our experiment, highlights how cache management can affect performance, even in seemingly race condition-free scenarios.
References: